Параграф 2. Повторение и расширение сведений о функции.
Работу выполнила: Казанцева А.А. студентка группы 45.2
Пункт 2.2. Свойства и графики основных функций.



Объяснение и обоснование
1. Линейная функция y = kx + b.Линейной функцией называется функция вида
y = kx + b, где k и b — некоторые числа.
Обоснуем основные характеристики этой функции: область определения, область
значений, четность или нечетность, возрастание и убывание.
Область определения — множество всех действительных чисел: D (y) = R,
поскольку формула kx + b имеет смысл при всех действительных значениях
x, то есть для любого действительного x мы можем вычислить значение
kx + b (из свойств действительных чисел, которые строго доказываются в
курсах математического анализа, следует, что для любых действительных
чисел х, k и b однозначно определены произведение kх и сумма kх + b = у).
Область значений линейной функции будет разной в зависимости от зна-
чения коэффициента k. 
Если k = 0, то функция имеет вид y = b, то есть ее
область значений состоит из одного числа b. В таком
случае графиком линейной функции y = b является
прямая, параллельная оси Ox, которая пересекает
ось Oy в точке b (рис. 19).
Если k ≠ 0, то E (y) = R (обоснование приведено в примере 3).
Четность и нечетность линейной функции существенно
зависит от значений коэффициентов b и k.
При b = 0 и k ≠ 0 функция y = kx + b превращается в функцию y = kx,
которая является нечетной, поскольку для всех x из ее области определения
Таким образом, график функции y = kx (рис. 22) симметричен относительно
точки O. 
При k = 0 получаем функцию y = b, которая является
четной, поскольку для всех x из ее области определения
f (-x) = b = f (x). То есть график функции y = b
симметричен относительно оси Oy (рис. 21).
В общем случае при k ≠ 0 и b ≠ 0 функция
y = kx + b не является ни четной, ни нечетной, поскольку
f (-x) = k (-x) + b = -kx + b ≠ f (x) и также
f (-x) = -kx + b = -(kx - b) ≠ -f (x).
Возрастание и убывание линейной функции зависит от значения коэффициента k.
При k = 0 получаем функцию y = b — постоянную. При k > 0 функция y = kx + b
возрастает, а при k < 0 — убывает (обоснование приведено в примере 4).
В курсе геометрии было показано, что графиком линейной функции y = kx + b всегда является прямая линия.
Поскольку при x = 0 функция принимает значение y = b, то эта прямая всегда
пересекает ось Oy в точке b. Графики линейных функций приведены в таблице 3/
2. Функция y = k/x (k ≠ 0).
Эта функция выражает обратно пропорциональную зависимость.
Область определения: х ≠ 0. Это можно записать также так:
Область значений: у Ф 0. Это можно записать также так:
Для обоснования области значений функции y = k/x обозначим k/x = a.
Тогда из этого равенства получим x = k/a для всех a ≠ 0. То есть
для всех a ≠ 0 существует значение x = k/a, при котором
y =k/x = k/(k/a) = a. Таким образом, y принимает все
действительные значения, не равные нулю.
Функция нечетная, поскольку ее областью определения является множество,
симметричное относительно точки О, и f (-x) = -k/x = -f(x). Таким образом,
её график симметричен относительно начала координат (рис. 23).
Возрастание и убывание функции зависит от знака коэффициента k.
Если х2 > х1 (то есть х2 — х1 > 0), то для сравнения значений f(х2) и f(х1)
рассмотрим их разность: f(x2)-f(x1) = k/x2 - k/x1 = -k(x2-x1)/x2x1.
На промежутке (0; +∞) значение х1 > 0 и х2 > 0, следовательно, х1х2 > 0.
На промежутке (-∞;0) значение х1 < 0 и х2 < 0, значит, х1х2 > 0.
Учитывая, что х2 — х1 > 0 на каждом из промежутков (—∞; 0) или (0; +∞), при
k > 0 из равенства (1) получаем f(х2) — f(х1) < 0, а при k < 0 получаем f(х2) — f(х1) > 0.
При k > 0 на каждом из промежутков (—∞; 0) и (0; +∞), если х2 > х1, то f (х2) < f (х1),
таким образом, функция убывает на каждом из этих промежутков.
При k < 0 на каждом из промежутков (—∞; 0) и (0; +∞), если х2 > х1, то f (х2) > f (х1),
следовательно, функция возрастает на каждом из этих промежутков.
Из курса алгебры известно, что график функции у = k/x называется
гиперболой (она состоит из двух ветвей). При k > 0 ветви гиперболы
находятся в I и III координатных четвертях, а при k < 0 — во II и IV четвертях (рис. 23).
Замечание. Характеризируя возрастание или убывание функции у = k/x (k ≠ 0),
следует помнить, что, например, функция у = 1/x (рис. 24) убывает
каждом из промежутков (—∞; 0) и (0; +∞), но на всей области определения (х ≠ 0)
эта функция не является убывающей (и не является возрастающей).
Действительно, если взять х1 = —1 и х2 = 1, то x2 > x1, но f(x2) = f(1) = 1, а f(x1) = f(—1) = —1,
то есть большему значению аргумента не соответствует меньшее значение функции,
и на всей ее области определения функция f(x) = 1/x не является убывающей.
Поэтому же нельзя сказать, что функция f (x) = 1/x — убывает на
объединении интервалов (—∞; 0) U (0; +∞). 
3. Функция y = ax² (a ≠ 0).Как известно из курса алгебры, графиком этой
функции является парабола, ветви которой направлены вверх при а > 0 (рис. 25, а)
и вниз при а < 0 (рис. 25, б). Поскольку при х = 0 значение у = 0, то график
всегда проходит через начало координат. 
<Область определения: х ∈ R, поскольку значение у = ах² можно вычислить при
любых значениях х (из свойств действительных чисел, которые строго
доказываются в курсах математического анализа, следует, что для любых
действительных чисел х и а однозначно определены произведения х • х = х2 и ах²
и ax² = y).
Функция четная, поскольку f (—x) = а (—х)² = ах² = f (x). Таким образом, ее
график симметричен относительно оси Оу.
Область значений. Для нахождения области значений функции у = ax²
обозначим ax² = u. Поскольку а ≠ 0, то из этого равенства x² = u/a (*). При а > 0
уравнение (*) имеет решение для любого u ≥ 0, а при а < 0 уравнение (*) имеет
решение для любого u ≤ 0.
Следовательно, при а > 0 Е (у) = [0; +∞), а при а < 0 Е (у) = (—∞; 0].
Возрастание и убывание.
Если x2 > x1 ( то есть x2 - x1 >0), то для сравнения значений y(x2) и y(x1) рассмотрим их разность
y(x2)-y(x1) = ax2² - ax1² = a(x2² - x1²) = a(x2-x1)(x2+x1). (2)
На промежутке [0; +∞) значение х1 ≥ 0 и х2 > 0, следовательно, х2 + х1 > 0.
На промежутке (—∞; 0] значение х1 < 0 и х2 ≤ 0, значит, х2 + х1 < 0.
Учитывая, что х2 — х1 > 0 на каждом из указанных промежутков, из равенства (2)
получаем:
- при a > 0 на промежутке [0; +∞) у (х2) — у (х1) > 0, а на промежутке (—∞; 0]
y(x2) - y(x1) < 0.
- при a < 0 на промежутке [0; +∞) у (х2) — у (х1) < 0, а на промежутке (—∞; 0]
y(x2) - y(x1) > 0.
Следовательно, при х2 > х1, если a > 0, то на промежутке [0; +∞) у(х2) > y(x1)
функция возрастает, а на промежутке (—∞; 0] у (х2) < у (х1) функция убывает.
если же a < 0, то на промежутке [0; +∞) у (х2) < у (х1)
функция убывает, а на промежутке (—∞; 0] у (х2) > у (х1) функция возрастает.
Соответствующие графики приведены также в таблице 3.
4. Квадратичная функция y = ax² + bx + c (a ≠ 0).
Из курса агебры за 9 класс известно, что функция вида
y = ax² + bx +c, где a,b,c - действительные числа, причём
a≠0, называется квадратичной.Ее графиком является парабола,
ветви которой направлены вверх при а > 0 и вниз при а < 0.
Абсцисса вершины этой параболы x0 =-b/2a. Для обоснования этого
достаточно в заданном квадратном трехчлене выделить полный квадрат:
y = ax² + bx + c = a(x² + (b/a)x + c/a) = a(x + b/2a)² + (4ac - b²)/4a, то есть
y = ax² + bx + c = a(x + b/2a)² + y0, где y0 = (4ac - b²)/4a = -D/4a (3)
(D = b² - 4ac - дискриминант квадратного треёхчлена ax² + bx + c).
Напомним, что в зависимости от знака дискриминанта D парабола или
пересекает ось Ох (D > 0), или не пересекает (D < 0), или касается ее (D = 0).
Основные варианты расположения графика функции у = ax²2 + bx + с (a ≠ 0)
представлены в таблице 4.
Охарактеризуем свойства функции у = ax² + bx + с (a ≠ 0).
Область определения: D (у) = R, поскольку значение у = ax²2 + bx + с (a ≠ 0)
можно вычислить при любых значениях х (из свойств действительных чисел,
которые строго доказываются в курсах математического анализа, следует, что для
любых действительных чисел х, а, b и с однозначно определены произведения
х • х = х&, ах² и bx и суммы ах² + bx, (ax² + bx) + с = ax² + bx + с = у).
Область значений. Для нахождения области значений функции у = ax² + bx + с
используем формулу (3) и обозначим a(x + b/2a)² + y0 = u. Поскольку a ≠ 0, то
из этого равенства: (x + b/2a)² = (u - y0)/a. 


ВОПРОСЫ ДЛЯ КОНТРОЛЯ:
1.Какая функция называется линейной? Назовите свойства линейной функции.
Какая линия является графиком линейной функции? Приведите примеры
линейных функций и их графиков.
2. Какая линия является графиком функции у = k/x (k≠ 0)? Приведите
графиков функций у = k/x при k > 0 и при k < 0. По графикам
укажите свойства этой функции при k > 0 и при k < 0. Докажите нечетность
функции у = k/x (k≠ 0).
3. Какая линия является графиком функции у = ax² (a ≠ 0)?
Как расположен этот график при а > 0 и при а < 0? Приведите примеры графиков функций
у = ax² при а > 0 и при а < 0. По графикам укажите свойства этой
функции при а > 0 и при а < 0. Докажите четность функции у = ax² (a ≠ 0).
4. Какая линия является графиком функции у = ax²2 + bx + с (a ≠ 0)?
Как расположен график при а > 0 и при а < 0? Как найти абсциссу
вершины графика функции у = ax²2 + bx + с (a ≠ 0)?
Приведите примеры графиков этой функции при а > 0 и при а < 0.
По графикам укажите свойства этой функции при а > 0 и при а < 0.
ПРИМЕРЫ РЕШЕНИЯ ПРАКТИЧЕСКИХ ЗАДАНИЙ
| УПРАЖНЕНИЕ 1. Постройте график функции: 1.y = 2x + 1 2.y = -3x - 1 3. y = 4 |
|
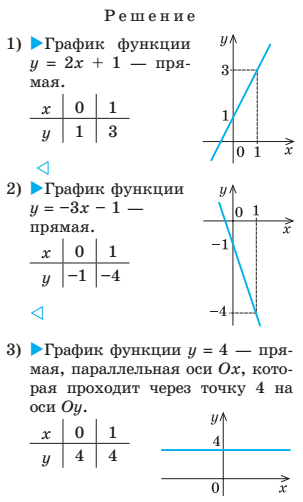 |
 |
|
УПРАЖНЕНИЕ 2. По приведённому графику функции y= kx+b укажите знаки k и b. |
|
 |
 |
| УПРАЖНЕНИЕ 3. Постройте график функции y = x² - 4x + 3. | |
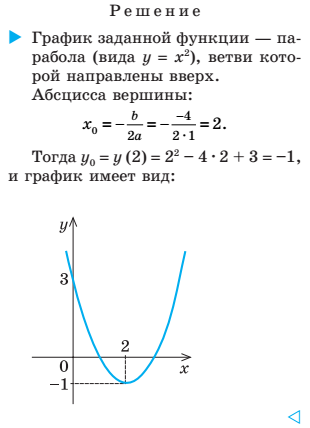 |
 |
УПРАЖНЕНИЯ К ПАРАГРАФУ
1. Постройте график функции:
1) y = 3x - 2; 2)y = -x + 4; 3) y = -2 4) y = -5x 5) y = 0 6)y = 4x
Есть ли среди этих функций чётные или нечётные? Ответ обоснуйте.
2. По приведёнными графикам функций y = kx + b (рис. 26) укажите знаки k и b в каждом случае. 
Постройте график функции (3 - 5 ).
3. 1) y = -2/x; 2) y = 3/x 3) y = 1/x 4) y = 5/x
4. 1) y = -2x² 2) y = 3x² 3) y = -3x² 4) y = 5x²
5. 1) y = x² - 6x + 7 2) y = -x² + 4x + 2 3) y = 2x² - 2x + 1 4) y = -3x² + 6x
6. По приведённым графикам функции y = ax² + bx + c (a≠) (рис. 27)
укажите знаки a, b, c в каждом случае. 

