Определение и графики тригонометрических функций

1.      Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.

2.      К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс,котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.

3.      Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.

4.      Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r: 
sinα=y/r. 
Поскольку r=1, то синус равен ординате точки M(x,y).

5.      Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r: 
cosα=x/r 

6.      Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x: 
tanα=y/x,x≠0 

7.      Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y: 
cotα=x/y,y≠0 

8.      Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y): 
secα=r/x=1/x,x≠0 

9.      Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y): 
cscα=r/y=1/y,y≠0 

10.  В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом: 
Синусом угла α называется отношение противолежащего катета к гипотенузе. 
Косинусом угла α называется отношение прилежащего катета к гипотенузе. 
Тангенсом угла α называется противолежащего катета к прилежащему. 
Котангенсом угла α называется прилежащего катета к противолежащему. 
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету. 
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету. 

11.  График функции синус 
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1 

12.  График функции косинус 
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1 

13.  График функции тангенс 
y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞<tanx<∞ 

14.  График функции котангенс 
y=cotx, область определения: x∈R,x≠kπ, область значений: −∞<cotx<∞ 

15.  График функции секанс 
y=secx, область определения: x∈R,x≠(2k+1)π/2, область значений:secx∈(−∞,−1]∪[1,∞) 

16.  График функции косеканс 
y=cscx, область определения: x∈R,x≠kπ, область значений: cscx∈(−∞,−1]∪[1,∞) 

Где применяется тригонометрия

Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей. Следует отметить применение в таких областях как: астрономия, физика, природа, биология, музыка, медицина и многие другие.

Тригонометрия в астрономии:

Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.

Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.

Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1—2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии. Он повысил точность наблюдений, применив для наведения на светило крест нитей в угломерных инструментах — секстантах и квадрантах. Ученый составил огромный по тем временам каталог положений 850 звезд, разделив их по блеску на 6 степеней (звездных величин). Гиппарх ввел географические координаты — широту и долготу, и его можно считать основателем математической географии. (ок. 190 до н. э. — ок. 120 до н. э.)

Достижения Виета в тригонометрии 
Полное решение задачи об определении всех элементов плоского или сферического треугольников по трем данным элементам, важные разложения sin пх и cos пх по степеням cos х и sinx. Знание формулы синусов и косинусов кратных дуг дало возможность Виету решить уравнение 45-й степени, предложенное математиком А. Рооменом; Виет показал, что решение этого уравнения сводится к разделению угла на 45 равных частей и что существуют 23 положительных корня этого уравнения. Виет решил задачу Аполлония с помощью линейки и циркуля.
Решение сферических треугольников- одна из задач астрономии Вычислять стороны и углы любого сферического треугольника по трем подходящим образом заданным сторонам или углам позволяют следующие теоремы: (теорема синусов) (теорема косинусов для углов) (теорема косинусов для сторон).

Тригонометрия в физике:

В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений.

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:

Где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая частота колебаний,   — полная фаза колебаний, r  — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде x’’ + ω²x = 0.

Механические колебания . Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примерами простых механических колебательных систем могут служить груз на пружине или математический маятник.

Тригонометрия в природе.

Мы часто задаем вопрос «Почему мы иногда видим то, чего нет на самом деле?». Для исследования предложены следующие вопросы: «Как возникает радуга? Северное сияние?», «Что такое оптические иллюзии?» ,«Как тригонометрия может помочь найти ответы на эти вопросы?».

Впервые теория радуги была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях.

Северное сияние Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.

Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.

Многофункциональная тригонометрия

·         Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения.

·         К тому же в биологии используется такое понятие как синус сонный, синус каротидный и венозный или пещеристый синус.

·         Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца - комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.

Тригонометрия и тригонометрические функции в медицине и биологии.

·         Одно из фундаментальных свойств живой природы - это цикличность большинства происходящих в ней процессов.

·         Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.

·         Основной земной ритм – суточный.

·         Модель биоритмов можно построить с помощью тригонометрических функций.

Тригонометрия в биологии

Какие биологические процессы связаны с тригонометрией?

·         Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца - комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.

·         Биологические ритмы, биоритмы связаны с тригонометрией

Связь биоритмов с тригонометрией

·         Модель биоритмов можно построить с помощью графиков тригонометрических функций. Для этого необходимо ввести дату рождения человека ( день, месяц, год ) и длительность прогноза

Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.

При полёте птицы траектория взмаха крыльев образует синусоиду.

Возникновение музыкальной гармонии

·         Согласно дошедшим из древности преданиям, первыми, кто попытался сделать это, были Пифагор и его ученики.

·         Частоты, соответствующие одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…

·         диатоническая гамма 2:3:5

Тригонометрия в архитектуре

·         Детская школа Гауди в Барселоне

·         Страховая корпорация Swiss Re в Лондоне

·         Феликс Кандела Ресторан в Лос-Манантиалесе

Значения тригонометрических функций

Ключевые слова: радиан, радианная мера угла, тригонометрическая окружность, знаки тригонометрических функций

В геометрии угол определяется как часть плоскости, ограниченная двумя лучами. 
При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота. 
Возьмем на координатной плоскости окружность радиуса R с центром O в начале координат. 
Пусть одна сторона угла  с вершиной в начале координат O идет по оси абсцисс, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси абсцисс. 
Из геометрии известно, что отношение длины дуги l , на которую опирается этот угол, к радиусу R этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла: =lR.

Такая мера называется радианной мерой угла и используется наравне с угловой. 
Говорят, что угол равен определенному числу радиан. 
Ясно, что угол в один радиан опирается на длину дуги окружности, равную её радиусу. 
В самом деле: =RR=1 радиан. Обозначение радиана – «рад». 
Так как длина всей окружности радиуса R равна 2R , то всей окружности соответствует угол =R2R=2 радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует 2360=180 градусов: 
1рад=1805717. И наоборот, 1=180рад.

Значит, можно написать следующие формулы перехода от градусного измерения к радианному: 
=180рад 

и от радианного измерения к градусному: 
=180 .

Обозначение «рад» при записи часто опускают и вместо, например, 180° =  рад пишут просто 180° = .

Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.

Так как, синус по определению равен ординате точки на единочной окружности, а косинус - абсциссе, то знаки тригонометрических функций по четвертям будут такими:

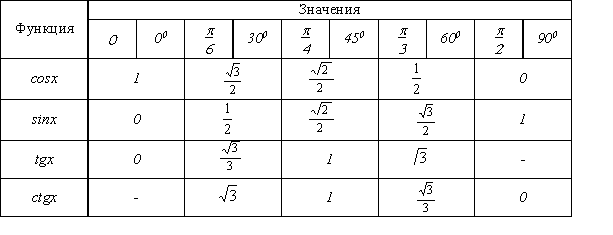
Вычисление тригонометрических функций некоторых углов.

Тригонометрические функции числового и углового аргументов

Тригонометрические функции числового аргумента.

Тригонометрические функции числового аргумента t  – это функции вида y = cos t, 
y = sin t, y = tg t, y = ctg t.

С помощью этих формул через известное значение одной тригонометрической функции можно найти неизвестные значения других тригонометрических функций.

Пояснения.

1) Возьмем формулу cos² t + sin² t = 1 и выведем с ее помощью новую формулу.

Для этого разделим обе части формулы на cos² t (при t ≠ 0, то есть t ≠ π/2 + πk). Итак:

  cos² t        sin² t             1
——— + ———  =  ———
 cos² t        cos² t          cos² t

Первое слагаемое равно 1. Мы знаем, что отношение синуса к конисусу – это тангенс, значит, второе слагаемое равно tg² t. В результате мы получаем новую (и уже известную вам) формулу:

2) Теперь разделим cos² t + sin² t = 1 на sin² t (при t ≠ πk):

  cos² t        sin² t             1
——— + ———  =  ———,   где t ≠ πk + πk, k – целое число
  sin² t         sin² t          sin² t

Отношение косинуса к синусу – это котангенс. Значит:

Зная элементарные основы математики и выучив основные формулы тригонометрии, вы легко сможете самостоятельно выводить большинство остальных тригонометрических тождеств. И это даже лучше, чем просто зазубривать их: выученное наизусть быстро забывается, а понятое запоминается надолго, если не навсегда. К примеру, необязательно зазубривать, чему равна сумма единицы и квадрата тангенса. Забыли – можно легко вспомнить, если вы знаете самую простую вещь: тангенс – это отношение синуса к косинусу. Примените вдобавок простое правило сложения дробей с разными знаменателями – и получите результат:

                           sin² t         1         sin² t          cos² t + sin² t             1
1 + tg² t  =  1 + ———  =  —  +  ———  =  ——————  =  ———
                          cos² t         1          cos² t               cos² t                cos² t

Точно так же легко можно найти сумму единицы и квадрата котангенса, как и многие другие тождества.

Тригонометрические функции углового аргумента.

В функциях  у = cos t, у = sin t, у = tg t, у = ctg t переменная t может быть не только числовым аргументом. Ее можно считать и мерой угла – то есть угловым аргументом.

С помощью числовой окружности и системы координат можно легко найти синус, косинус, тангенс, котангенс любого угла. Для этого должны быть соблюдены два важных условия: 
1) вершиной угла должен быть центр окружности, который одновременно является центром оси координат;

2) одной из сторон угла должен быть положительный луч оси x.

В этом случае ордината точки, в которой пересекаются окружность и вторая сторона угла, является синусом этого угла, а абсцисса этой точки – косинусом данного угла.

Пояснение. Нарисуем угол, одна сторона которого – положительный луч оси x, а вторая сторона выходит из начала оси координат (и из центра окружности) под углом 30º (см.рисунок). Тогда точка пересечения второй стороны с окружностью соответствует π/6. Нам известны ордината и абсцисса этой точки. Они же являются косинусом и синусом нашего угла:

   √3       1
 ——; ——
    2        2

  А зная синус и косинус угла, вы уже легко сможете найти его тангенс и котангенс.

Таким образом, числовая окружность, расположенная в системе координат, является удобным способом найти синус, косинус, тангенс или котангенс угла.

Но есть более простой способ. Можно и не рисовать окружность и систему координат. Можно воспользоваться простыми и удобными формулами:

Пример: найти синус и косинус угла, равного 60º.

Решение:

                        π · 60                π         √3
sin 60º  =  sin ———  =  sin —— = ——
                         180                  3          2

                           π        1
cos 60º  =  cos —— = —
                           3        2